Kolejne dodawanie znaków char, aby uzyskać najdłuższe słowo w słowniku

Question

Podano słownik słów i początkowy znak. znajdź najdłuższe możliwe słowo w słowniku, dodając kolejno do niego znak. W danym przypadku słowo powinno być poprawnym słowem w słowniku.

ex: a -> w -> cat -> koszyk -> wykres ....

Answer 1

Podejście brute force byłoby spróbować dodanie listy do każdego dostępnego indeksu za pomocą przeszukiwanie w głąb.

Tak więc, zaczynając od "a", istnieją dwa miejsca, w których można dodać nową literę. Z przodu lub z tyłu "a", reprezentowane przez kropki poniżej.

.a.

Jeśli dodać 'T', istnieją obecnie trzy pozycje.

.a.t.

Można spróbować dodać wszystkie 26 liter do każdej dostępnej pozycji. Słownik w tym przypadku może być prostym hashtable. Jeśli dodasz "z" w środku, otrzymasz "azt", który nie będzie w hashtable, więc nie będziesz kontynuował tej ścieżki w wyszukiwaniu.

Edytuj: Wykres Nicka Johnsona sprawił, że byłem ciekawy, jak mógłby wyglądać wykres wszystkich maksymalnych ścieżek. Jest to duży (1,6 MB) obraz tutaj:

http://www.michaelfogleman.com/static/images/word_graph.png

Edit: Oto implementacja Pythona. Metoda brute-force działa w rozsądnym czasie (kilka sekund, w zależności od litery początkowej).

import heapq 

letters = 'abcdefghijklmnopqrstuvwxyz' 

def search(words, word, path): 
    path.append(word) 
    yield tuple(path) 
    for i in xrange(len(word)+1): 
     before, after = word[:i], word[i:] 
     for c in letters: 
      new_word = '%s%s%s' % (before, c, after) 
      if new_word in words: 
       for new_path in search(words, new_word, path): 
        yield new_path 
    path.pop() 

def load(path): 
    result = set() 
    with open(path, 'r') as f: 
     for line in f: 
      word = line.lower().strip() 
      result.add(word) 
    return result 

def find_top(paths, n): 
    gen = ((len(x), x) for x in paths) 
    return heapq.nlargest(n, gen) 

if __name__ == '__main__': 
    words = load('TWL06.txt') 
    gen = search(words, 'b', []) 
    top = find_top(gen, 10) 
    for path in top: 
     print path 

Oczywiście w odpowiedzi będzie wiele powiązań. Spowoduje to wydrukowanie najlepszych wyników N, mierzonych długością ostatniego słowa.

Wyjście dla litery początkowej "a", przy użyciu słownika Scrabble TWL06.

(10, ('a', 'ta', 'tap', 'tape', 'taped', 'tamped', 'stamped', 'stampede', 'stampedes', 'stampeders')) 
(10, ('a', 'ta', 'tap', 'tape', 'taped', 'tamped', 'stamped', 'stampede', 'stampeder', 'stampeders')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'strangle', 'strangles', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'strangle', 'strangler', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranges', 'strangles', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranges', 'strangers', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranges', 'strangers', 'estrangers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranges', 'estranges', 'estrangers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranger', 'strangler', 'stranglers')) 
(10, ('a', 'ta', 'tan', 'tang', 'stang', 'strang', 'strange', 'stranger', 'strangers', 'stranglers')) 

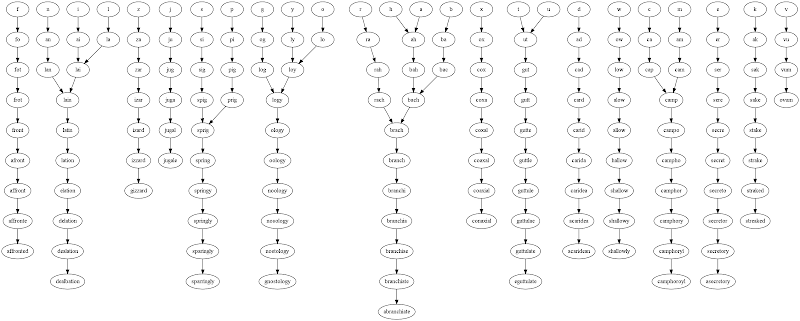
Oto wyniki dla każdej litery początkowej. Oczywiście wyjątek jest taki, że pojedyncza litera początkowa nie musi znajdować się w słowniku. Tylko jakieś 2-literowe słowo, które można z niego utworzyć.

(10, ('a', 'ta', 'tap', 'tape', 'taped', 'tamped', 'stamped', 'stampede', 'stampedes', 'stampeders')) 
(9, ('b', 'bo', 'bos', 'bods', 'bodes', 'bodies', 'boodies', 'bloodies', 'bloodiest')) 
(1, ('c',)) 
(10, ('d', 'od', 'cod', 'coed', 'coped', 'comped', 'compted', 'competed', 'completed', 'complected')) 
(10, ('e', 're', 'rue', 'ruse', 'ruses', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(9, ('f', 'fe', 'foe', 'fore', 'forge', 'forges', 'forgoes', 'forgoers', 'foregoers')) 
(10, ('g', 'ag', 'tag', 'tang', 'stang', 'strang', 'strange', 'strangle', 'strangles', 'stranglers')) 
(9, ('h', 'sh', 'she', 'shes', 'ashes', 'sashes', 'slashes', 'splashes', 'splashers')) 
(11, ('i', 'pi', 'pin', 'ping', 'oping', 'coping', 'comping', 'compting', 'competing', 'completing', 'complecting')) 
(7, ('j', 'jo', 'joy', 'joky', 'jokey', 'jockey', 'jockeys')) 
(9, ('k', 'ki', 'kin', 'akin', 'takin', 'takins', 'takings', 'talkings', 'stalkings')) 
(10, ('l', 'la', 'las', 'lass', 'lassi', 'lassis', 'lassies', 'glassies', 'glassines', 'glassiness')) 
(10, ('m', 'ma', 'mas', 'mars', 'maras', 'madras', 'madrasa', 'madrassa', 'madrassas', 'madrassahs')) 
(11, ('n', 'in', 'pin', 'ping', 'oping', 'coping', 'comping', 'compting', 'competing', 'completing', 'complecting')) 
(10, ('o', 'os', 'ose', 'rose', 'rouse', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(11, ('p', 'pi', 'pin', 'ping', 'oping', 'coping', 'comping', 'compting', 'competing', 'completing', 'complecting')) 
(3, ('q', 'qi', 'qis')) 
(10, ('r', 're', 'rue', 'ruse', 'ruses', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(10, ('s', 'us', 'use', 'uses', 'ruses', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(10, ('t', 'ti', 'tin', 'ting', 'sting', 'sating', 'stating', 'estating', 'restating', 'restarting')) 
(10, ('u', 'us', 'use', 'uses', 'ruses', 'rouses', 'arouses', 'carouses', 'carousels', 'carrousels')) 
(1, ('v',)) 
(9, ('w', 'we', 'wae', 'wake', 'wakes', 'wackes', 'wackest', 'wackiest', 'whackiest')) 
(8, ('x', 'ax', 'max', 'maxi', 'maxim', 'maxima', 'maximal', 'maximals')) 
(8, ('y', 'ye', 'tye', 'stye', 'styed', 'stayed', 'strayed', 'estrayed')) 
(8, ('z', 'za', 'zoa', 'zona', 'zonae', 'zonate', 'zonated', 'ozonated')) 

Answer 2

Jeśli chcesz to zrobić raz, zrobiłbym następujące (uogólnione problemu zaczynając z pełnym słowa):

Zabierz całą słownika i wyrzucić wszystko, co nie ma nadzbiór znaków w twoim docelowym słowie (powiedzmy, że ma długość m). Następnie odrzuć pozostałe słowa według długości. Dla każdego słowa o długości m+1 spróbuj upuścić każdą literę i sprawdź, czy to daje pożądane słowo. Jeśli nie, rzuć to. Następnie sprawdź każde słowo o długości m+2 w stosunku do prawidłowego zbioru o długości m+1, pomijając te, których nie można zmniejszyć. Idź dalej, aż znajdziesz pusty zestaw; ostatnia rzecz, którą znalazłeś, będzie najdłuższa.

Jeśli chcesz szybko to sprawdzić, zbuduję drzewo przyrostków - , takie jak struktura danych.

Grupuj wszystkie słowa według długości. Dla każdego słowa o długości 2 umieść każdą z jego dwóch postaci w zestawie "podword" i dodaj to słowo do każdego zestawu znaków "superword". Teraz masz link pomiędzy wszystkimi poprawnymi słowami o długości 2 i wszystkimi znakami. Zrób to samo ze słowami o długości 3 i prawidłowymi słowami o długości 2. Teraz możesz zacząć od dowolnego miejsca w tej hierarchii i wykonać szerokie pierwsze wyszukiwanie, aby znaleźć najgłębszą gałąź.

---

Edit: prędkość tego rozwiązania będzie zależał w dużym stopniu od struktury języka, ale jeśli zdecydujemy się zbudować wszystko używając zestawów z log(n) wykonania wszystkich operacji (czyli używamy czerwono-czarny drzew lub podobnych), a my mamy N(m) słów o długości m, a następnie, aby utworzyć połączenie między słowami o długości m+1 i, czas około (biorąc pod uwagę, że ciąg porównuje wziąć liniowy czas w długości łańcucha). Skoro mamy to zrobić dla wszystkich długości tekstu, środowisko wykonawcze do budowania pełnej struktury danych będzie czymś na porządku

(typical word length)^3 * (dictionary length) * log (dictionary length/word length) 

(Początkowy binningu w słowach pewnej długości wymaga czasu liniowego tak może być zaniedbane, rzeczywista formuła dla środowiska wykonawczego jest skomplikowana, ponieważ zależy od rozkładu długości słów, ponieważ przypadek, w którym robisz to z jednego słowa, jest jeszcze bardziej skomplikowany, ponieważ zależy od oczekiwanej liczby dłuższych słów, które mają krótsze podszewki .)

Answer 3

Zakładając, że musisz to zrobić wielokrotnie (lub chcesz uzyskać odpowiedź na każdą z 26 liter), zrób to od tyłu:

1. obciążenia słownikiem i sortować je według długości, malejąco
2. ustanowienie mapy, początkowo pusta, między słowami i (rozszerzających, max_len) krotek.
3. Dla każdego słowa w liście posortowanej:
   1. Jeśli jest już w mapowaniu, pobrać max len.
   2. Jeśli nie, ustaw maks. Długość len na długość słowa.
   3. Sprawdź każde słowo utworzone przez usunięcie znaku. Jeśli słowo nie jest w mapowaniu, czy nasz max_len przekracza max_len słowa już w mapowaniu zaktualizować mapowanie z bieżącego słowa i max_len

Następnie, aby uzyskać łańcuch dla danego prefiks, po prostu zacznij od tego prefiksu i powtarzaj go w słowniku.

Oto przykładowy kod Python:

words = [x.strip().lower() for x in open('/usr/share/dict/words')] 
words.sort(key=lambda x:len(x), reverse=True) 
word_map = {} # Maps words to (extension, max_len) tuples 

for word in words: 
    if word in word_map: 
    max_len = word_map[word][1] 
    else: 
    max_len = len(word) 
    for i in range(len(word)): 
    new_word = word[:i] + word[i+1:] 
    if new_word not in word_map or word_map[new_word][2] < max_len: 
     word_map[new_word] = (word, max_len) 

# Get a chain for each letter 
for term in "abcdefghijklmnopqrstuvwxyz": 
    chain = [term] 
    while term in word_map: 
    term = word_map[term][0] 
    chain.append(term) 
    print chain 

a jego wyjście dla każdej litery alfabetu:

['a', 'ah', 'bah', 'bach', 'brach', 'branch', 'branchi', 'branchia', 'branchiae', 'branchiate', 'abranchiate'] 
['b', 'ba', 'bac', 'bach', 'brach', 'branch', 'branchi', 'branchia', 'branchiae', 'branchiate', 'abranchiate'] 
['c', 'ca', 'cap', 'camp', 'campo', 'campho', 'camphor', 'camphory', 'camphoryl', 'camphoroyl'] 
['d', 'ad', 'cad', 'card', 'carid', 'carida', 'caridea', 'acaridea', 'acaridean'] 
['e', 'er', 'ser', 'sere', 'secre', 'secret', 'secreto', 'secretor', 'secretory', 'asecretory'] 
['f', 'fo', 'fot', 'frot', 'front', 'afront', 'affront', 'affronte', 'affronted'] 
['g', 'og', 'log', 'logy', 'ology', 'oology', 'noology', 'nosology', 'nostology', 'gnostology'] 
['h', 'ah', 'bah', 'bach', 'brach', 'branch', 'branchi', 'branchia', 'branchiae', 'branchiate', 'abranchiate'] 
['i', 'ai', 'lai', 'lain', 'latin', 'lation', 'elation', 'delation', 'dealation', 'dealbation'] 
['j', 'ju', 'jug', 'juga', 'jugal', 'jugale'] 
['k', 'ak', 'sak', 'sake', 'stake', 'strake', 'straked', 'streaked'] 
['l', 'la', 'lai', 'lain', 'latin', 'lation', 'elation', 'delation', 'dealation', 'dealbation'] 
['m', 'am', 'cam', 'camp', 'campo', 'campho', 'camphor', 'camphory', 'camphoryl', 'camphoroyl'] 
['n', 'an', 'lan', 'lain', 'latin', 'lation', 'elation', 'delation', 'dealation', 'dealbation'] 
['o', 'lo', 'loy', 'logy', 'ology', 'oology', 'noology', 'nosology', 'nostology', 'gnostology'] 
['p', 'pi', 'pig', 'prig', 'sprig', 'spring', 'springy', 'springly', 'sparingly', 'sparringly'] 
['q'] 
['r', 'ra', 'rah', 'rach', 'brach', 'branch', 'branchi', 'branchia', 'branchiae', 'branchiate', 'abranchiate'] 
['s', 'si', 'sig', 'spig', 'sprig', 'spring', 'springy', 'springly', 'sparingly', 'sparringly'] 
['t', 'ut', 'gut', 'gutt', 'gutte', 'guttle', 'guttule', 'guttulae', 'guttulate', 'eguttulate'] 
['u', 'ut', 'gut', 'gutt', 'gutte', 'guttle', 'guttule', 'guttulae', 'guttulate', 'eguttulate'] 
['v', 'vu', 'vum', 'ovum'] 
['w', 'ow', 'low', 'alow', 'allow', 'hallow', 'shallow', 'shallowy', 'shallowly'] 
['x', 'ox', 'cox', 'coxa', 'coxal', 'coaxal', 'coaxial', 'conaxial'] 
['y', 'ly', 'loy', 'logy', 'ology', 'oology', 'noology', 'nosology', 'nostology', 'gnostology'] 
['z', 'za', 'zar', 'izar', 'izard', 'izzard', 'gizzard'] 

EDIT: Biorąc pod uwagę stopień, w jakim gałęzie scalić ku końcowi, myślałem, że byłoby interesujące narysować wykres pokazujący to:

Ciekawe przedłużenie tego wyzwania: Prawdopodobnie istnieje kilka ostatecznych słów równości dla niektórych liter.Który zestaw łańcuchów minimalizuje liczbę końcowych węzłów (np. Łączy najwięcej liter)?