Oblicz kąt potrzebny do trafienia współrzędnych (x, y) z pozycji innej niż (0,0) z różną wysokością

Question

Próbuję obliczyć kąt wymagany do wystrzelenia pocisku, aby trafić określoną współrzędną.

Mój pocisk znajduje się losową współrzędną i moją docelową współrzędną na statycznej współrzędnej.

skończyło się biegnącą przez następujące równanie Wikipedia obliczania kąta wymagane trafić na współrzędnych (x, y), z (0,0)

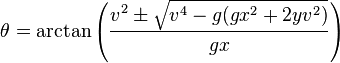
dokonaniu kilku prób zrozumieć tę i inną formułę i próbowałem następującej implementacji (używam C# i XNA).

double y = source.Y - target.Y; 
double x = Vector2.Distance(source, target); 
double v = 1440; //velocity 
double g = 25; //gravity 
double sqrt = (v*v*v*v) - (g*(g*(x*x) + 2*y*(v*v))); 
sqrt = Math.Sqrt(sqrt); 
double angleInRadians = Math.Atan(((v*v) + sqrt)/(g*x)); 

Podjęłam również próbę, która dała taki sam kąt, w którym wartości v i g pozostają takie same.

double targetX = target.X - source.X; 
double targetY = -(target.Y - source.Y); 
double r1 = Math.Sqrt((v*v*v*v) - g*(g*(target.X*target.X) + ((2*target.Y)*(v*v)))); 
double a1 = ((v*v) + r1)/(g*target.X); 
angleInRadians = -Math.Atan(a1); 
if (targetX < 0) 
{ 
    angleInRadians -= 180/180*Math.PI; 
} 

Moja hipoteza jest taka, że ​​nawet w moim (założonym) próbując się do zera współrzędnych źródła, że ​​ja wciąż nie wykonując obliczenia poprawnie współrzędnych z nie (0,0) źródła i różnych wysokościach.

Poniżej znajduje się obraz przedstawiający mój układ współrzędnych. Jest to ustawienie domyślne dla XNA.

Answer 1

Dzięki pomocy w komentarzach Rozwiązaniem znaleźć kąt ten zakończył się wymagająca, że ​​pozycje być przetłumaczony na (0,0) system oparty. Dla każdego, kto szuka tego samego scenariusza finału Roztwór roboczy:

double x = -(source.x - target.x); 
double y = (source.y - target.y); 
double v = 1440; //m/s 
double g = 25; //m/s 
double sqrt = (v*v*v*v) - (g*(g*(x*x) + 2*y*(v*v))); 
sqrt = Math.Sqrt(sqrt); 
angleInRadians = Math.Atan(((v*v) + sqrt)/(g*x)); 

Następnie do konwersji radiany do wektora, który współpracuje z XNA, wykonaj następujące przekształcenia:

Vector2 angleVector = new Vector2(-(float)Math.Cos(angleInRadians), (float)Math.Sin(angleInRadians)); 

Answer 2

Myślę, że prawdziwym problemem polega na użyciu arctan. Ponieważ zakres jest ograniczony do -pi/2.ppi/2 wyniki są tylko w prawej półpłaszczyźnie.

Zastosowanie arctan2 aby uzyskać odpowiednie współrzędne:

angleInRadians = Math.Atan2(((v*v) + tmp), (g*x));